Introduction of Stack
A stack is a fundamental data structure in computer science that operates in a Last-In-First-Out (LIFO) manner. This means that the last element added to the stack is the first one to be removed. Stacks are used in various applications, such as evaluating expressions, backtracking algorithms, and managing function calls.
Key Characteristics of a Stack
- LIFO (Last-In-First-Out): The most recently added element is the first to be removed.
- Operations:
- Push: Add an element to the top of the stack.
- Pop: Remove the top element from the stack.
- Peek (or Top): Return the top element without removing it.
- isEmpty: Check if the stack is empty.
- Use Cases:
- Function Call Management: Stacks are used in programming languages for keeping track of function calls and local variables. The call stack is a stack that stores information about active subroutines.
- Expression Evaluation: Stacks are used in algorithms for evaluating arithmetic expressions (e.g., infix to postfix conversion).
- Undo Mechanisms: Stacks are used in applications like text editors to keep track of changes for undo operations.
- Backtracking Algorithms: Stacks are useful in algorithms that involve backtracking, such as solving mazes or puzzles like the Tower of Hanoi.
Advantages and Disadvantages
Advantages:
- Simple and easy to implement.
- Efficient for LIFO operations.
Disadvantages:
- Limited access to only the top element.
- Not suitable for scenarios where random access is needed.
Stacks are an essential concept in data structures and algorithms, providing a simple yet powerful mechanism for managing data in a controlled manner. Understanding stacks is crucial for problem-solving and software development.
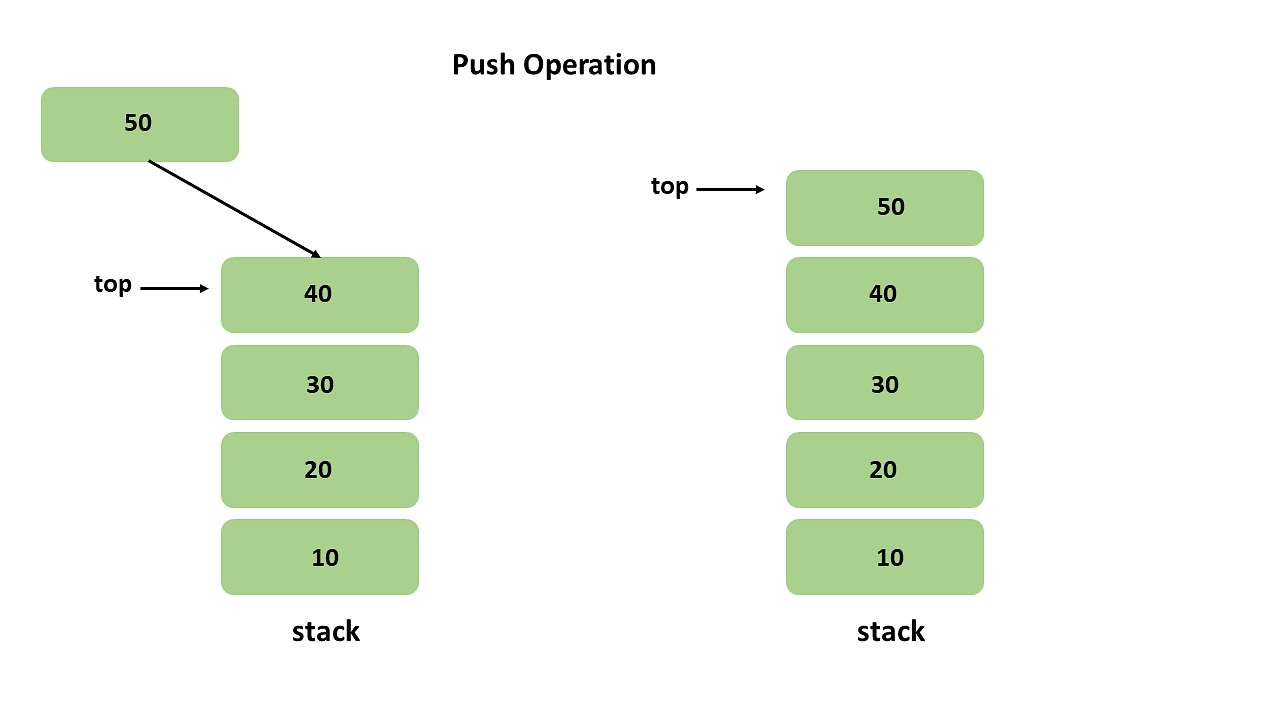
Push operations
The push operation adds a new element to the top of the stack. This is like stacking plates in a cafeteria: when you add a new plate, you place it on top of the stack of plates.
Here are the steps involved in the push operation:
- Check for Space:
- Ensure there is room for a new element. In fixed-size stacks, this means checking for overflow (when the stack is full).
- Add the Element:
- Place the new element on top of the current stack.
- Update the Top:
- Adjust the top pointer or index to reflect the new element’s position.
Example program on push operation
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
// Define the maximum size of the stack
#define MAX_SIZE 5
// Define the stack structure
typedef struct {
int items[MAX_SIZE]; // Array to store stack elements
int top; // Index of the top element
} Stack;
// Function to initialize the stack
void initStack(Stack* s) {
s->top = -1; // The stack is initially empty
}
// Function to check if the stack is full
bool isFull(Stack* s) {
return s->top == MAX_SIZE - 1; // Returns true if the top is at the last index
}
// Function to check if the stack is empty
bool isEmpty(Stack* s) {
return s->top == -1; // Returns true if the top is at the initial position
}
// Function to push an element onto the stack
void push(Stack* s, int item) {
// Check for overflow
if (isFull(s)) {
printf("Stack overflow: Cannot push %d onto the stack.\n", item);
return;
}
// Increment the top index and add the item
s->top++;
s->items[s->top] = item;
// Print the current state of the stack
printf("Pushed %d: Current stack: ", item);
for (int i = 0; i <= s->top; i++) {
printf("%d ", s->items[i]);
}
printf("\n");
}
// Main function to demonstrate the push operation
int main() {
Stack stack;
initStack(&stack); // Initialize the stack
// Push elements onto the stack
push(&stack, 10);
push(&stack, 20);
push(&stack, 30);
push(&stack, 40);
push(&stack, 50);
push(&stack, 60); // This will cause a stack overflow
return 0;
}–>Click here for detail Explanation of Push operation
Preprocessor Directives:
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <stdio.h>: Includes the standard input-output library, which provides functions likeprintfandscanf.#include <stdlib.h>: Includes the standard library, providing utility functions like memory allocation (not used here but useful in other contexts).#include <stdbool.h>: Allows the use of thebooldata type for boolean values (trueandfalse).
Define Maximum Stack Size:
#define MAX_SIZE 5
- This macro defines the maximum number of elements the stack can hold. The stack is fixed in size with this limit.
Stack Structure:
typedef struct {
int items[MAX_SIZE]; // Array to store stack elements
int top; // Index of the top element
} Stack;
items: An array to store the stack’s elements.top: An integer tracking the index of the top element in the stack. Initially set to-1, indicating the stack is empty.
Initialize the Stack:
void initStack(Stack* s) {
s->top = -1; // The stack is initially empty
}
- The function initializes the stack by setting the
topindex to-1.
Check if the Stack is Full:
bool isFull(Stack* s) {
return s->top == MAX_SIZE - 1; // Returns true if the top is at the last index
}
- The function checks whether the stack is full by comparing
topwithMAX_SIZE - 1.
Check if the Stack is Empty:
bool isEmpty(Stack* s) {
return s->top == -1; // Returns true if the top is at the initial position
}
- The function checks whether the stack is empty by comparing
topwith-1.
Push Operation:
void push(Stack* s, int item) {
// Check for overflow
if (isFull(s)) {
printf("Stack overflow: Cannot push %d onto the stack.\n", item);
return;
}
// Increment the top index and add the item
s->top++;
s->items[s->top] = item;
// Print the current state of the stack
printf("Pushed %d: Current stack: ", item);
for (int i = 0; i <= s->top; i++) {
printf("%d ", s->items[i]);
}
printf("\n");
}
- Check for Overflow: The function checks if the stack is full using
isFull(). If full, it prints an overflow message and returns. - Increment Top: The
topindex is incremented to point to the next available position. - Add Item: The new item is added to the position pointed to by
top. - Print Stack: The current state of the stack is printed to show the elements.
Main Function:
int main() {
Stack stack;
initStack(&stack); // Initialize the stack
// Push elements onto the stack
push(&stack, 10);
push(&stack, 20);
push(&stack, 30);
push(&stack, 40);
push(&stack, 50);
push(&stack, 60); // This will cause a stack overflow
return 0;
}
Push Operations: Calls push() to add elements to the stack, demonstrating normal operations and an overflow condition.
Initialize Stack: Calls initStack to set up the stack.
Pop operation
The pop operation is used to remove the top element of the stack.
Steps to Perform the Pop Operation:
- Check for Underflow:
- Before attempting to pop an element, check if the stack is empty by checking if
topis-1. - If the stack is empty, report an underflow error since there is no element to pop.
- Before attempting to pop an element, check if the stack is empty by checking if
- Access the Top Element:
- Retrieve the element at the index
topin the array, as this is the element to be removed.
- Retrieve the element at the index
- Update the Top Index:
- Decrement the
topindex by 1 to point to the next element in the stack. - This effectively removes the element from the stack by no longer keeping track of it.
- Decrement the
- Return the Popped Element:
- Return the element that was removed for any further use or processing.
Program for Pop operation
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
// Define the maximum size of the stack
#define MAX_SIZE 5
// Define the stack structure
typedef struct {
int items[MAX_SIZE]; // Array to store stack elements
int top; // Index of the top element
} Stack;
// Function to initialize the stack
void initStack(Stack* s) {
s->top = -1; // The stack is initially empty
}
// Function to check if the stack is full
bool isFull(Stack* s) {
return s->top == MAX_SIZE - 1; // Returns true if the top is at the last index
}
// Function to check if the stack is empty
bool isEmpty(Stack* s) {
return s->top == -1; // Returns true if the top is at the initial position
}
// Function to push an element onto the stack
void push(Stack* s, int item) {
// Check for overflow
if (isFull(s)) {
printf("Stack overflow: Cannot push %d onto the stack.\n", item);
return;
}
// Increment the top index and add the item
s->top++;
s->items[s->top] = item;
// Print the current state of the stack
printf("Pushed %d: Current stack: ", item);
for (int i = 0; i <= s->top; i++) {
printf("%d ", s->items[i]);
}
printf("\n");
}
// Function to pop an element from the stack
int pop(Stack* s) {
// Check for underflow
if (isEmpty(s)) {
printf("Stack underflow: Cannot pop from an empty stack.\n");
return -1; // Return a sentinel value to indicate failure
}
// Retrieve the top element and decrement the top index
int poppedItem = s->items[s->top];
s->top--;
// Print the current state of the stack
printf("Popped %d: Current stack: ", poppedItem);
for (int i = 0; i <= s->top; i++) {
printf("%d ", s->items[i]);
}
printf("\n");
return poppedItem; // Return the popped element
}
// Main function to demonstrate the pop operation
int main() {
Stack stack;
initStack(&stack); // Initialize the stack
// Push elements onto the stack
push(&stack, 10);
push(&stack, 20);
push(&stack, 30);
push(&stack, 40);
push(&stack, 50);
// Pop elements from the stack
pop(&stack);
pop(&stack);
pop(&stack);
pop(&stack);
pop(&stack);
pop(&stack); // This will cause a stack underflow
return 0;
}–>Click here for detail Explanation for Pop operation program
Preprocessor Directives:
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
- Includes the standard input-output library, standard library, and boolean type.
Define Maximum Stack Size:
#define MAX_SIZE 5
- Defines the maximum number of elements the stack can hold.
Stack Structure:
typedef struct {
int items[MAX_SIZE]; // Array to store stack elements
int top; // Index of the top element
} Stack;
- Defines the stack structure with an array and a
topindex.
Initialize the Stack:
void initStack(Stack* s) {
s->top = -1; // The stack is initially empty
}
- Initializes the stack by setting the
topindex to-1.
Check if the Stack is Full:
bool isFull(Stack* s) {
return s->top == MAX_SIZE - 1; // Returns true if the top is at the last index
}
- Checks whether the stack is full.
Check if the Stack is Empty:
bool isEmpty(Stack* s) {
return s->top == -1; // Returns true if the top is at the initial position
}
- Checks whether the stack is empty.
Push Operation:
void push(Stack* s, int item) {
// Check for overflow
if (isFull(s)) {
printf("Stack overflow: Cannot push %d onto the stack.\n", item);
return;
}
// Increment the top index and add the item
s->top++;
s->items[s->top] = item;
// Print the current state of the stack
printf("Pushed %d: Current stack: ", item);
for (int i = 0; i <= s->top; i++) {
printf("%d ", s->items[i]);
}
printf("\n");
}
- Pushes an element onto the stack, checking for overflow.
Pop Operation:
int pop(Stack* s) {
// Check for underflow
if (isEmpty(s)) {
printf("Stack underflow: Cannot pop from an empty stack.\n");
return -1; // Return a sentinel value to indicate failure
}
// Retrieve the top element and decrement the top index
int poppedItem = s->items[s->top];
s->top--;
// Print the current state of the stack
printf("Popped %d: Current stack: ", poppedItem);
for (int i = 0; i <= s->top; i++) {
printf("%d ", s->items[i]);
}
printf("\n");
return poppedItem; // Return the popped element
}
- Check for Underflow: The function checks if the stack is empty using
isEmpty(). If empty, it prints an underflow message and returns-1(a sentinel value to indicate failure). - Retrieve Top Element: Retrieves the element at the top of the stack.
- Decrement Top Index: Decrements the
topindex to point to the new top element after popping. - Print Stack: Prints the current state of the stack.
- Return Popped Element: Returns the popped element.
Main Function:
int main() {
Stack stack;
initStack(&stack); // Initialize the stack
// Push elements onto the stack
push(&stack, 10);
push(&stack, 20);
push(&stack, 30);
push(&stack, 40);
push(&stack, 50);
// Pop elements from the stack
pop(&stack);
pop(&stack);
pop(&stack);
pop(&stack);
pop(&stack);
pop(&stack); // This will cause a stack underflow
return 0;
}
Initializes the stack, performs several push operations, and then performs pop operations, demonstrating normal operation and an underflow condition.
Stack Over flow and Under flow
Overflow in Stacks
Overflow occurs when trying to add (push) an element to a stack that is already full.
1. Array-Based Stack Overflow
In an array-based stack, the size is fixed and predetermined, which means the stack has a maximum capacity defined by the size of the array.
How Overflow Occurs:
- Condition: The overflow condition happens when the
topindex reaches the maximum size of the array (MAX_SIZE - 1). - Attempted Operation: A
pushoperation is attempted on a full stack.
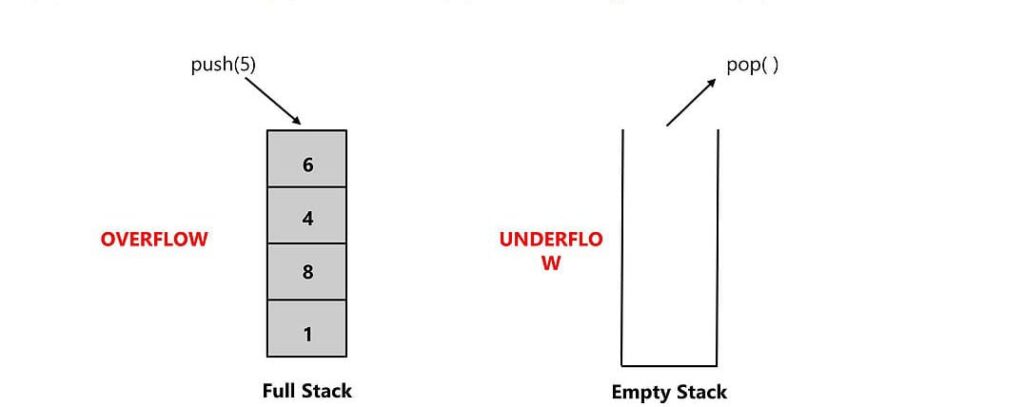
Underflow in Stacks
Underflow occurs when trying to remove (pop) an element from a stack that is already empty.
1. Array-Based Stack Underflow
In an array-based stack, underflow occurs when there are no elements left to pop.
How Underflow Occurs:
- Condition: The stack is empty when
topis-1. - Attempted Operation: A
popoperation is attempted on an empty stack.
Linked list implementation of a Stack
Implementing a stack using a linked list is a flexible and dynamic approach that allows the stack to grow and shrink as needed without a fixed size limit. Let’s go through a detailed implementation of a stack using a linked list in C, including the basic operations like push, pop, and peek.
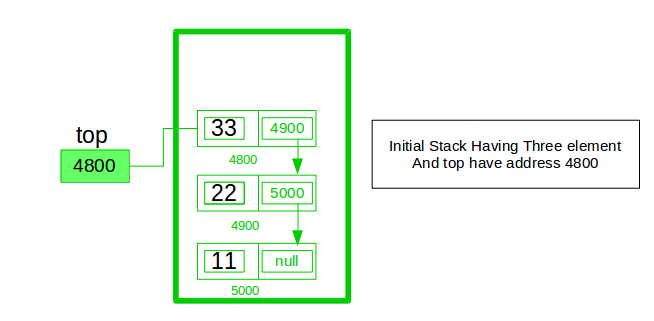
To implement a stack using a singly linked list, we leverage the LIFO (Last In, First Out) principle, where operations are performed at the “head” of the list. Here’s how it works:
- Top Pointer: In our stack implementation, the
toppointer represents the head of the list. This is where both pushing and popping operations occur. - Linked List Structure: Each node in the linked list contains:
- Data Field: Stores the element of the stack.
- Link Field: Points to the next node in the list.
- The
toppointer points to the first node in the list, and the link field of the last node isNULL.
Advantages of Using a Linked List for Stack Implementation
- Dynamic Size: Unlike arrays, a linked list allows the stack to grow and shrink dynamically without a fixed capacity.
- No Overflow: Since memory is allocated dynamically for each node, stack overflow due to a fixed array size is avoided.
Stack Operations
push(): Adds a new element to the top of the stack.- Steps:
- Initialize a new node.
- Set the node’s data field to the new value.
- Link this node to the current top node.
- Update the
toppointer to point to the new node.
- Steps:
pop(): Removes and returns the top element of the stack.- Steps:
- Check if the stack is empty. If it is, report an underflow condition.
- Access the top node.
- Update the
toppointer to the next node in the list. - Free the memory allocated for the old top node.
- Return the data from the removed node.
- Steps:
peek(): Returns the top element without removing it.- Steps:
- Check if the stack is empty. If it is, report an underflow condition.
- Return the data from the node pointed to by the
toppointer.
- Steps:
display(): Prints all elements in the stack.- Steps:
- Start from the top node.
- Traverse the list, printing each node’s data until reaching the end of the list.
- Steps:
Program for linked list Implementation of a stack and it’s operation
#include <stdio.h>
#include <stdlib.h>
// Define the Node structure
typedef struct Node {
int data; // Data stored in the node
struct Node* next; // Pointer to the next node
} Node;
// Define the Stack structure
typedef struct Stack {
Node* top; // Pointer to the top node of the stack
} Stack;
// Function to initialize the stack
void initStack(Stack* s) {
s->top = NULL; // The stack is initially empty
}
// Function to check if the stack is empty
int isEmpty(Stack* s) {
return s->top == NULL;
}
// Function to push an element onto the stack
void push(Stack* s, int item) {
// Step 1: Create a new node
Node* newNode = (Node*)malloc(sizeof(Node));
if (!newNode) {
printf("Memory allocation failed: Cannot push %d onto the stack.\n", item);
return;
}
// Step 2: Set the new node's data
newNode->data = item;
// Step 3: Link the new node to the current top node
newNode->next = s->top;
// Step 4: Update the top pointer to the new node
s->top = newNode;
// Print confirmation of the push operation
printf("Pushed %d onto the stack.\n", item);
}
// Function to pop an element from the stack
int pop(Stack* s) {
// Check for underflow
if (isEmpty(s)) {
printf("Stack underflow: Cannot pop from an empty stack.\n");
return -1; // Return a sentinel value to indicate failure
}
// Access the top node and store its data
Node* temp = s->top;
int poppedItem = temp->data;
// Update the top pointer to the next node
s->top = s->top->next;
// Free the old top node
free(temp);
// Return the popped item
printf("Popped %d from the stack.\n", poppedItem);
return poppedItem;
}
// Function to peek at the top element of the stack
int peek(Stack* s) {
if (isEmpty(s)) {
printf("Stack is empty: Cannot peek.\n");
return -1; // Return a sentinel value to indicate failure
}
// Return the data of the top node
return s->top->data;
}
// Function to display all elements in the stack
void display(Stack* s) {
if (isEmpty(s)) {
printf("Stack is empty.\n");
return;
}
Node* current = s->top;
printf("Stack elements:\n");
while (current != NULL) {
printf("%d\n", current->data);
current = current->next;
}
}
// Main function to demonstrate stack operations
int main() {
Stack stack;
initStack(&stack); // Initialize the stack
// Push elements onto the stack
push(&stack, 10);
push(&stack, 20);
push(&stack, 30);
push(&stack, 40);
push(&stack, 50);
// Peek at the top element
printf("Top element: %d\n", peek(&stack));
// Display all elements in the stack
display(&stack);
// Pop elements from the stack
pop(&stack);
pop(&stack);
// Peek again
printf("Top element after popping: %d\n", peek(&stack));
// Display remaining elements in the stack
display(&stack);
return 0;
}–>Click here for detail explanation of linked list Implementation of a stack and it’s operation
1. Node Structure
The Node structure represents a single element in the stack and is defined as follows:
typedef struct Node {
int data; // The data stored in the node
struct Node* next; // Pointer to the next node in the list
} Node;
data: This integer field holds the value of the element stored in the node.next: This pointer points to the next node in the linked list. If it’s the last node,nextwill beNULL.
2. Stack Structure
The Stack structure maintains the stack’s state and is defined as follows:
typedef struct Stack {
Node* top; // Pointer to the top node of the stack
} Stack;
top: This pointer points to the top node of the stack, which is the head of the linked list. It represents the most recently added element.
3. Functions and Their Details
a. Initialize the Stack
Function: initStack
void initStack(Stack* s) {
s->top = NULL; // The stack is initially empty
}
- Purpose: Sets up the stack by initializing the
toppointer toNULL, indicating that the stack is empty. - Operation: When a stack is initialized, no nodes are present, so the
topisNULL.
b. Check if the Stack is Empty
Function: isEmpty
int isEmpty(Stack* s) {
return s->top == NULL;
}
- Purpose: Determines if the stack is empty.
- Operation: Returns
1(true) iftopisNULL, meaning there are no elements in the stack. Otherwise, returns0(false).
c. Push Operation
Function: push
void push(Stack* s, int item) {
Node* newNode = (Node*)malloc(sizeof(Node));
if (!newNode) {
printf("Memory allocation failed: Cannot push %d onto the stack.\n", item);
return;
}
newNode->data = item;
newNode->next = s->top;
s->top = newNode;
printf("Pushed %d onto the stack.\n", item);
}
- Purpose: Adds a new element to the top of the stack.
- Steps:
- Allocate Memory:
mallocallocates memory for a new node. If memory allocation fails, an error message is printed. - Set Data:
newNode->datais assigned the value of the element to be pushed. - Link Node:
newNode->nextis set to the current top node (i.e., the node that was previously on top of the stack). - Update Top:
s->topis updated to point tonewNode, making it the new top of the stack.
- Allocate Memory:
- Result: The new node becomes the new top of the stack, and the previous top is now the second node in the list.
d. Pop Operation
Function: pop
int pop(Stack* s) {
if (isEmpty(s)) {
printf("Stack underflow: Cannot pop from an empty stack.\n");
return -1; // Return a sentinel value to indicate failure
}
Node* temp = s->top;
int poppedItem = temp->data;
s->top = s->top->next;
free(temp);
printf("Popped %d from the stack.\n", poppedItem);
return poppedItem;
}
- Purpose: Removes and returns the element from the top of the stack.
- Steps:
- Check for Underflow: Uses
isEmptyto ensure the stack is not empty. If it is, prints an error message and returns-1. - Access Top Node:
tempis assigned the current top node. - Retrieve Data:
poppedItemstores the data of the node being removed. - Update Top:
s->topis updated to point to the next node in the list. - Free Memory: The memory of the old top node is deallocated using
free.
- Check for Underflow: Uses
- Result: The top element is removed, and the stack’s top pointer now points to the next node.
e. Peek Operation
Function: peek
int peek(Stack* s) {
if (isEmpty(s)) {
printf("Stack is empty: Cannot peek.\n");
return -1; // Return a sentinel value to indicate failure
}
return s->top->data;
}
- Purpose: Returns the top element of the stack without removing it.
- Steps:
- Check if Empty: Uses
isEmptyto ensure the stack is not empty. If it is, prints an error message and returns-1. - Return Data: Returns the data from the node pointed to by
top.
- Check if Empty: Uses
- Result: The top element’s value is returned without modifying the stack.
f. Display Operation
Function: display
void display(Stack* s) {
if (isEmpty(s)) {
printf("Stack is empty.\n");
return;
}
Node* current = s->top;
printf("Stack elements:\n");
while (current != NULL) {
printf("%d\n", current->data);
current = current->next;
}
}
- Purpose: Prints all elements in the stack from top to bottom.
- Steps:
- Check if Empty: Uses
isEmptyto ensure the stack is not empty. If it is, prints a message and exits the function. - Traverse List: Starts from the
topnode and prints thedataof each node. - Move to Next Node: Updates
currentto the next node until reaching the end of the list (currentbecomesNULL).
- Check if Empty: Uses
- Result: All elements are printed in order from the top of the stack to the bottom.
Main Function
Function: main
int main() {
Stack stack;
initStack(&stack); // Initialize the stack
push(&stack, 10);
push(&stack, 20);
push(&stack, 30);
push(&stack, 40);
push(&stack, 50);
printf("Top element: %d\n", peek(&stack));
display(&stack);
pop(&stack);
pop(&stack);
printf("Top element after popping: %d\n", peek(&stack));
display(&stack);
return 0;
}
- Initialization: Creates a stack and initializes it using
initStack. - Push Operations: Adds several elements to the stack.
- Peek Operation: Displays the top element of the stack.
- Display Operation: Prints all elements in the stack.
- Pop Operations: Removes two elements from the stack.
- Peek and Display Again: Shows the top element after popping and displays the remaining elements.
This detailed explanation covers the stack implementation using a singly linked list, describing the purpose and steps of each function and how they interact with the stack’s structure.
Applications of stacks
1. Function Call Management (Call Stack)
- Description: The call stack manages function calls and local variables during program execution.
- How It Works:
- When a function is called, a stack frame (containing return address and local variables) is pushed onto the call stack.
- When the function returns, the stack frame is popped, and control returns to the calling function.
- Benefits: Helps in managing function calls and recursion, and tracks return addresses.
2. Expression Evaluation
- Description: Stacks are used to evaluate expressions, especially in infix, prefix, and postfix notations.
- Infix Expression: Operators are between operands (e.g.,
A + B). - Prefix Expression: Operators precede operands (e.g.,
+ A B). - Postfix Expression: Operators follow operands (e.g.,
A B +). - How It Works:
- Postfix Evaluation: Uses a stack to store operands until an operator is encountered, which then performs operations on the top operands.
- Conversion: Infix expressions are converted to postfix using a stack to handle operator precedence and parentheses.
3. Undo Mechanism in Software
- Description: Many software applications (like text editors) use stacks to implement the undo feature.
- How It Works:
- Each action (like typing or deleting text) is pushed onto a stack.
- When undo is requested, the most recent action is popped from the stack and reversed.
4. Backtracking Algorithms
- Description: Stacks are used in algorithms that involve exploring multiple possibilities and then reverting changes (backtracking).
- Examples: Maze solving, puzzle solving (like Sudoku or the Eight Queens problem).
- How It Works:
- As the algorithm explores paths or solutions, it pushes the current state onto a stack.
- If a path doesn’t work, it pops the stack to revert to a previous state and tries another path.
5. Depth-First Search (DFS) in Graphs
- Description: DFS is a graph traversal algorithm that uses a stack to explore vertices.
- How It Works:
- Starts at a vertex, pushes it onto the stack, and explores adjacent vertices.
- Continues until all vertices are explored or the stack is empty.
6. Syntax Parsing
- Description: Stacks are used in syntax parsing to validate and process code in compilers and interpreters.
- How It Works:
- Parsing: Stack-based parsers (like LL parsers) use stacks to handle nested structures like parentheses and brackets.
- Balancing Symbols: Used to ensure that symbols (like braces in programming languages) are properly nested and balanced.
7. String Reversal
- Description: Stacks can reverse a string by pushing characters onto the stack and then popping them off in reverse order.
- How It Works:
- Push each character of the string onto the stack.
- Pop characters off the stack to get the reversed string.
8. Arithmetic Expression Conversion
- Description: Stacks are used to convert arithmetic expressions from infix to prefix or postfix notation.
- How It Works:
- Infix to Postfix Conversion: Uses a stack to manage operators and parentheses according to their precedence and associativity rules.
9. Memory Management
- Description: In some memory management schemes, stacks are used to manage memory allocation and deallocation.
- How It Works:
- Function Call Stack: Keeps track of function calls, local variables, and return addresses.
- Dynamic Memory Allocation: Some memory allocators use stacks to manage memory blocks and allocation requests.
10. Algorithms and Data Structures
- Description: Several algorithms and data structures rely on stacks.
- Examples:
- Infix to Postfix Conversion: As mentioned before, converting expressions using stacks.
- Tower of Hanoi: Solving the Tower of Hanoi problem can be done using a stack-based approach.
Summary
Stacks are fundamental in various domains of computer science, from managing function calls and implementing undo functionality to parsing expressions and exploring algorithms. Their LIFO (Last In, First Out) nature makes them well-suited for scenarios where reversing operations and tracking state changes are essential.
Convert Infix Expression to postfix Expression
The idea is to use the stack data structure to convert an infix expression to a postfix expression. The stack is used to reverse the order of operators in postfix expression. The stack is also used to hold operators since an operator can’t be added to a postfix expression until both of its operands are processed.
Key Concepts
- Infix Expression: Operators are placed between operands (e.g.,
A + B). - Postfix Expression: Operators follow their operands (e.g.,
A B +).
Rules for Conversion
- Operands (e.g., variables and numbers) are added directly to the output.
- Operators (e.g.,
+,-,*,/) are pushed onto the stack, but only after popping operators with higher or equal precedence from the stack. - Parentheses are used to override the precedence:
- Left Parenthesis (
(): Push onto the stack. - Right Parenthesis (
)): Pop from the stack to the output until a left parenthesis is encountered.
- Left Parenthesis (
Precedence and Associativity
- Precedence: Determines the order of operations. For example,
*and/have higher precedence than+and-. - Associativity: Determines the order of operations for operators with the same precedence. Most operators are left-associative (evaluated left to right), but some (like exponentiation) are right-associative.
Implementation Steps
- Initialize: Create an empty stack for operators and an empty output list.
- Read the infix expression: Process each token (operand, operator, or parenthesis).
- Handle each token:
- Operand: Add it to the output list.
- Operator: Pop operators from the stack to the output list while the top of the stack has operators of higher or equal precedence. Push the current operator onto the stack.
- Left Parenthesis: Push it onto the stack.
- Right Parenthesis: Pop operators from the stack to the output list until a left parenthesis is encountered.
- After reading the infix expression: Pop any remaining operators from the stack to the output list.
Algorithm Steps
- Initialize:
- An empty stack for operators.
- An empty list for the output.
- Read Tokens:
- If Token is an Operand: Append it to the output list.
- If Token is a Left Parenthesis
(: Push it onto the stack. - If Token is a Right Parenthesis
): Pop from the stack to the output list until a left parenthesis is encountered. Discard the parentheses. - If Token is an Operator:
- Pop from the stack to the output list any operators that have higher or equal precedence than the current operator.
- Push the current operator onto the stack.
- End of Expression:
- Pop all operators from the stack to the output list.
To illustrate how the stack performs during the conversion of the infix expression A * (B * C + D * E) + F to postfix notation using boxes, we’ll walk through each token of the expression and show the state of the stack and output at each step.
Conversion Steps with Stack and Output Visualization
Infix Expression: A * (B * C + D * E) + F
Goal: Convert to Postfix Expression
1. Initial State:
- Stack: (empty)
- Output: (empty)
2. Process Each Token:
Token: A
- Action: Operand. Add directly to the output.
- Output:
A - Stack: (empty)
Token: *
- Action: Operator. Push onto the stack.
- Output:
A - Stack:markdownCopy code
*
Token: (
- Action: Left parenthesis. Push onto the stack.
- Output:
A - Stack:markdownCopy code
* (
Token: B
- Action: Operand. Add directly to the output.
- Output:
A B - Stack:markdownCopy code
* (
Token: *
- Action: Operator. Push onto the stack (inside parentheses).
- Output:
A B - Stack:markdownCopy code
* ( *
Token: C
- Action: Operand. Add directly to the output.
- Output:
A B C - Stack:markdownCopy code
* ( *
Token: +
- Action: Operator. Pop
*from the stack to the output (since+has lower precedence). Push+onto the stack. - Output:
A B C * - Stack:markdownCopy code
* ( +
Token: D
- Action: Operand. Add directly to the output.
- Output:
A B C * D - Stack:markdownCopy code
* ( +
Token: *
- Action: Operator. Push onto the stack (since
*has higher precedence than+). - Output:
A B C * D - Stack:markdownCopy code
* ( + *
Token: E
- Action: Operand. Add directly to the output.
- Output:
A B C * D E - Stack:markdownCopy code
* ( + *
Token: )
- Action: Right parenthesis. Pop all operators from the stack until a left parenthesis is encountered.
- Output:
A B C * D E * + - Stack:markdownCopy code
*
Token: +
- Action: Operator. Pop
*from the stack to the output (since+has lower precedence). Push+onto the stack. - Output:
A B C * D E * + * - Stack:diffCopy code
+
Token: F
- Action: Operand. Add directly to the output.
- Output:
A B C * D E * + F - Stack:diffCopy code
+
3. Finish Processing:
- Action: Pop all remaining operators from the stack and add them to the output.
- Output:
A B C * D E * + F + - Stack: (empty)
Summary of Stack and Output States
| Token | Stack | Output |
|---|---|---|
| A | A | |
| * | * | A |
| ( | * ( | A |
| B | * ( | A B |
| * | * ( * | A B |
| C | * ( * | A B C |
| + | * ( + | A B C * |
| D | * ( + | A B C * D |
| * | * ( + * | A B C * D |
| E | * ( + * | A B C * D E |
| ) | * | A B C * D E * + |
| + | + | A B C * D E * + * |
| F | + | A B C * D E * + F |
| End | A B C * D E * + F + |
Final Postfix Expression
Postfix Expression: A B C * D E * + F +
This step-by-step box-based visualization helps clarify how each token affects the stack and the output list, leading to the correct postfix notation.
Program for Conversion of Infix Expression to postfix Expression
#include <stdio.h>
#include <stdlib.h>
#include <ctype.h> // For isdigit function
#define MAX 100
// Stack data structure for operators
typedef struct {
int top;
char items[MAX];
} Stack;
// Function prototypes
void initStack(Stack* s);
int isEmpty(Stack* s);
void push(Stack* s, char c);
char pop(Stack* s);
char peek(Stack* s);
int precedence(char op);
int isOperator(char c);
void infixToPostfix(const char* infix, char* postfix);
void initStack(Stack* s) {
s->top = -1;
}
int isEmpty(Stack* s) {
return s->top == -1;
}
void push(Stack* s, char c) {
if (s->top < (MAX - 1)) {
s->items[++s->top] = c;
}
}
char pop(Stack* s) {
if (!isEmpty(s)) {
return s->items[s->top--];
}
return '\0'; // Return null character if stack is empty
}
char peek(Stack* s) {
if (!isEmpty(s)) {
return s->items[s->top];
}
return '\0'; // Return null character if stack is empty
}
int precedence(char op) {
switch (op) {
case '+':
case '-': return 1;
case '*':
case '/': return 2;
case '^': return 3;
default: return 0;
}
}
int isOperator(char c) {
return c == '+' || c == '-' || c == '*' || c == '/' || c == '^';
}
void infixToPostfix(const char* infix, char* postfix) {
Stack s;
initStack(&s);
int i = 0, k = 0;
while (infix[i] != '\0') {
if (isspace(infix[i])) {
i++;
continue; // Skip spaces
}
if (isdigit(infix[i])) {
// Process number (operand)
while (isdigit(infix[i])) {
postfix[k++] = infix[i++];
}
postfix[k++] = ' '; // Separate operands by space
} else if (infix[i] == '(') {
push(&s, infix[i++]);
} else if (infix[i] == ')') {
while (!isEmpty(&s) && peek(&s) != '(') {
postfix[k++] = pop(&s);
postfix[k++] = ' ';
}
pop(&s); // Pop the '(' from the stack
i++;
} else if (isOperator(infix[i])) {
while (!isEmpty(&s) && precedence(peek(&s)) >= precedence(infix[i])) {
postfix[k++] = pop(&s);
postfix[k++] = ' ';
}
push(&s, infix[i++]);
} else {
printf("Invalid character %c\n", infix[i]);
exit(EXIT_FAILURE);
}
}
// Pop remaining operators from the stack
while (!isEmpty(&s)) {
postfix[k++] = pop(&s);
postfix[k++] = ' ';
}
postfix[k - 1] = '\0'; // Remove the last space and null-terminate the string
}
int main() {
char infix[MAX] = "A * ( B * C + D * E ) + F";
char postfix[MAX];
infixToPostfix(infix, postfix);
printf("Postfix Expression: %s\n", postfix);
return 0;
}–>Click here for detail Explanation of Conversion of Infix Expression to postfix Expression program
1. Header Files and Definitions
#include <stdio.h>
#include <stdlib.h>
#include <ctype.h> // For isdigit function
#define MAX 100
<stdio.h>: Standard input/output functions.<stdlib.h>: Standard library functions, including memory allocation and program termination.<ctype.h>: For character handling functions likeisdigit()to check if a character is a digit.#define MAX 100: Defines a constantMAXto be used as the size of the stack and arrays.
2. Stack Data Structure
typedef struct {
int top;
char items[MAX];
} Stack;
Stack: A structure to represent the stack used for operators and parentheses.top: Index of the top element in the stack.items: Array to store stack elements.
3. Stack Functions
void initStack(Stack* s);
int isEmpty(Stack* s);
void push(Stack* s, char c);
char pop(Stack* s);
char peek(Stack* s);
initStack: Initializes the stack by setting the top index to -1, indicating an empty stack.isEmpty: Checks if the stack is empty by checking iftopis -1.push: Adds an element to the top of the stack, incrementing thetopindex.pop: Removes and returns the top element of the stack, decrementing thetopindex.peek: Returns the top element without removing it.
4. Operator Precedence and Validity
int precedence(char op);
int isOperator(char c);
precedence: Returns the precedence level of the operator:+and-have lower precedence (1).*and/have higher precedence (2).^(exponentiation) has the highest precedence (3).
isOperator: Checks if a character is an operator.
5. Infix to Postfix Conversion
void infixToPostfix(const char* infix, char* postfix);
infixToPostfix: Converts the infix expression to postfix notation using the Shunting Yard algorithm.
Detailed Steps Inside infixToPostfix
- Initialize Stack and Output Array
Stack s;
initStack(&s);
int i = 0, k = 0;
initStack(&s): Initializes the stack.i: Index for traversing the infix expression.k: Index for placing characters in the postfix expression.
- Process Each Token
while (infix[i] != '\0') {
if (isspace(infix[i])) {
i++;
continue; // Skip spaces
}
if (isdigit(infix[i])) {
while (isdigit(infix[i])) {
postfix[k++] = infix[i++];
}
postfix[k++] = ' '; // Separate operands by space
} else if (infix[i] == '(') {
push(&s, infix[i++]);
} else if (infix[i] == ')') {
while (!isEmpty(&s) && peek(&s) != '(') {
postfix[k++] = pop(&s);
postfix[k++] = ' ';
}
pop(&s); // Pop the '(' from the stack
i++;
} else if (isOperator(infix[i])) {
while (!isEmpty(&s) && precedence(peek(&s)) >= precedence(infix[i])) {
postfix[k++] = pop(&s);
postfix[k++] = ' ';
}
push(&s, infix[i++]);
} else {
printf("Invalid character %c\n", infix[i]);
exit(EXIT_FAILURE);
}
}
- Whitespace: Skip spaces.
- Operands: Add directly to the output, handling multi-digit operands.
- Left Parenthesis: Push onto the stack to signify the start of a sub-expression.
- Right Parenthesis: Pop from the stack to the output until a left parenthesis is encountered, then discard the left parenthesis.
- Operators: Pop from the stack to the output if operators on the stack have higher or equal precedence. Push the current operator onto the stack.
- Pop Remaining Operators
while (!isEmpty(&s)) {
postfix[k++] = pop(&s);
postfix[k++] = ' ';
}
postfix[k - 1] = '\0'; // Remove the last space and null-terminate the string
- Pop all remaining operators from the stack to the output.
- Remove the trailing space and null-terminate the postfix expression string.
6. Main Function
int main() {
char infix[MAX] = "A * ( B * C + D * E ) + F";
char postfix[MAX];
infixToPostfix(infix, postfix);
printf("Postfix Expression: %s\n", postfix);
return 0;
}
infix[MAX]: Contains the infix expression.postfix[MAX]: Array to store the resulting postfix expression.infixToPostfix: Converts the infix expression to postfix notation.printf: Prints the postfix expression.
Summary
- Initialization: Set up the stack and output array.
- Processing Tokens: Traverse the infix expression, handling operands, operators, and parentheses. Use the stack to manage operator precedence and parentheses.
- Finalization: Pop any remaining operators from the stack and format the output.
- Output: Print the converted postfix expression.
This detailed breakdown should give you a thorough understanding of how the program converts an infix expression to postfix notation.
Evaluate Postfix Expression
Evaluating a postfix expression (also known as Reverse Polish Notation) involves using a stack to process operands and operators. The postfix expression eliminates the need for parentheses to denote operation precedence, simplifying evaluation. Here’s a detailed explanation and a C program example for evaluating postfix expressions.
Steps to Evaluate a Postfix Expression
- Initialize an empty stack.
- Scan the postfix expression from left to right.
- Process Each Token:
- If the token is an operand (number), push it onto the stack.
- If the token is an operator (e.g.,
+,-,*,/):- Pop the required number of operands from the stack.
- Perform the operation using these operands.
- Push the result back onto the stack.
- After scanning the expression, the final result will be the only element left on the stack.
Evaluate a Postfix Expression
Evaluating a postfix expression (also known as Reverse Polish Notation) involves using a stack to process operands and operators. The postfix expression eliminates the need for parentheses to denote operation precedence, simplifying evaluation. Here’s a detailed explanation and a C program example for evaluating postfix expressions.
Steps to Evaluate a Postfix Expression
- Initialize an empty stack.
- Scan the postfix expression from left to right.
- Process Each Token:
- If the token is an operand (number), push it onto the stack.
- If the token is an operator (e.g.,
+,-,*,/):- Pop the required number of operands from the stack.
- Perform the operation using these operands.
- Push the result back onto the stack.
- After scanning the expression, the final result will be the only element left on the stack.
Algorithm to Evaluate Postfix Expression
- Initialize an empty stack.
- Scan the postfix expression from left to right.
- For each token in the postfix expression:
- If the token is an operand (number):
- Push it onto the stack.
- If the token is an operator (e.g.,
+,-,*,/):- Pop the required number of operands from the stack.
- Perform the operation with these operands.
- Push the result back onto the stack.
- If the token is an operand (number):
- After processing all tokens, the stack should contain only one element, which is the result of the postfix expression.
- Return the result from the stack.
Postfix Expression: 3 4 * 5 6 * +
Let’s represent the state of the stack and the process for each step:
Initial State
- Stack: (empty)
- Expression:
3 4 * 5 6 * +
Step-by-Step Process
1. Token: 3
- Action: Push
3onto the stack. - Stack:
| 3 | - Expression Remaining:
4 * 5 6 * +
2. Token: 4
- Action: Push
4onto the stack. - Stack:
| 4 | | 3 | - Expression Remaining:
* 5 6 * +
3. Token: *
- Action: Pop
4and3, compute3 * 4 = 12, push12. - Stack:
| 12 | - Expression Remaining:
5 6 * +
4. Token: 5
- Action: Push
5onto the stack. - Stack:
| 5 | | 12 | - Expression Remaining:
6 * +
5. Token: 6
- Action: Push
6onto the stack. - Stack:
| 6 | | 5 | | 12 | - Expression Remaining:
* +
6. Token: *
- Action: Pop
6and5, compute5 * 6 = 30, push30. - Stack:
| 30 | | 12 | - Expression Remaining:
+
7. Token: +
- Action: Pop
30and12, compute12 + 30 = 42, push42. - Stack:
| 42 | - Expression Remaining: (empty)
Final State:
- Stack:
42 - Result:
42
Summary of Algorithm with Boxes
- Initialize: Start with an empty stack.
- Processing Tokens:
- For operands, push onto the stack.
- For operators, pop the required number of operands from the stack, perform the operation, and push the result.
- Final Result: The last remaining value on the stack is the result.
Example program to Evaluate Postfix Expression
#include <stdio.h>
#include <stdlib.h>
#include <ctype.h> // For isdigit function
#define MAX 100
// Stack data structure for operands
typedef struct {
int top;
int items[MAX];
} Stack;
// Function prototypes
void initStack(Stack* s);
int isEmpty(Stack* s);
void push(Stack* s, int value);
int pop(Stack* s);
int peek(Stack* s);
int evaluatePostfix(const char* postfix);
void initStack(Stack* s) {
s->top = -1; // Initialize the stack as empty
}
int isEmpty(Stack* s) {
return s->top == -1; // Check if the stack is empty
}
void push(Stack* s, int value) {
if (s->top < (MAX - 1)) {
s->items[++s->top] = value; // Push value onto the stack
}
}
int pop(Stack* s) {
if (!isEmpty(s)) {
return s->items[s->top--]; // Pop and return the top value
}
return 0; // Return 0 if stack is empty (should handle this better in production code)
}
int peek(Stack* s) {
if (!isEmpty(s)) {
return s->items[s->top]; // Return the top value without removing it
}
return 0; // Return 0 if stack is empty
}
int evaluatePostfix(const char* postfix) {
Stack s;
initStack(&s);
int i = 0;
while (postfix[i] != '\0') {
// Skip spaces
if (isspace(postfix[i])) {
i++;
continue;
}
// Process number (operand)
if (isdigit(postfix[i])) {
int num = 0;
while (isdigit(postfix[i])) {
num = num * 10 + (postfix[i] - '0'); // Build the number
i++;
}
push(&s, num); // Push the number onto the stack
}
// Process operator
else if (postfix[i] == '+') {
int op2 = pop(&s); // Pop two operands
int op1 = pop(&s);
push(&s, op1 + op2); // Perform operation and push result
i++;
}
else if (postfix[i] == '-') {
int op2 = pop(&s);
int op1 = pop(&s);
push(&s, op1 - op2);
i++;
}
else if (postfix[i] == '*') {
int op2 = pop(&s);
int op1 = pop(&s);
push(&s, op1 * op2);
i++;
}
else if (postfix[i] == '/') {
int op2 = pop(&s);
int op1 = pop(&s);
push(&s, op1 / op2);
i++;
}
else {
printf("Invalid character %c\n", postfix[i]);
exit(EXIT_FAILURE);
}
}
return pop(&s); // The final result is the only element left in the stack
}
int main() {
char postfix[MAX] = "3 4 * 5 6 * +"; // Postfix expression
int result = evaluatePostfix(postfix); // Evaluate the expression
printf("Result of Postfix Expression: %d\n", result); // Print the result
return 0;
}–>Click here for detail Explanation of Evaluate Postfix Expression
Header Files and Definitions:
#include <stdio.h>
#include <stdlib.h>
#include <ctype.h> // For isdigit function
#define MAX 100
<stdio.h>: For input/output operations.<stdlib.h>: For standard library functions like memory allocation and program termination.<ctype.h>: For character functions such asisdigit()to check if a character is a digit.#define MAX 100: Sets a maximum size for the stack and arrays.
- Stack Data Structure:
typedef struct {
int top;
int items[MAX];
} Stack;
Stack: Structure to represent the stack used for operands.top: Index of the top element.items: Array to store stack elements.
- Stack Functions:
void initStack(Stack* s);
int isEmpty(Stack* s);
void push(Stack* s, int value);
int pop(Stack* s);
int peek(Stack* s);
initStack: Initializes the stack by settingtopto -1 (empty stack).isEmpty: Checks if the stack is empty by verifying iftopis -1.push: Adds a value to the stack, incrementing thetopindex.pop: Removes and returns the top value of the stack, decrementing thetopindex.peek: Returns the top value without removing it from the stack.
- Evaluate Postfix Expression:
int evaluatePostfix(const char* postfix);
evaluatePostfix: Converts and evaluates the postfix expression.- Loop through each character in the postfix expression.
- If a digit: Parse the entire number and push it onto the stack.
- If an operator: Pop the top two values, perform the operation, and push the result.
- Handle invalid characters: Print an error message and exit.
- Return the final result from the stack.
- Main Function:
int main() {
char postfix[MAX] = "3 4 * 5 6 * +";
int result = evaluatePostfix(postfix);
printf("Result of Postfix Expression: %d\n", result);
return 0;
}
- Defines a postfix expression.
- Calls
evaluatePostfixto compute the result. - Prints the result.
Summary
- Initialize: Start with an empty stack.
- Process Tokens:
- For operands (numbers), push them onto the stack.
- For operators, pop the required number of operands, perform the operation, and push the result.
- Final Result: The result of the postfix expression evaluation is the only value left on the stack.
This program effectively demonstrates how to evaluate postfix expressions using a stack in C, managing multiple operators and operands efficiently.
